Par défaut, les termes convectifs et les termes d’inertie et les termes convectifs sont négligés dans les calculs. Hydra propose cependant des options de calcul affinés permettant d'activer ces termes pour répondre à certaines applications spécifiques.
Les chapitres suivants présentent :
- les équations de Barré de Saint Venant en une et deux dimensions en identifiant les termes pouvant être ou non ignorés lors du calcul,
- les 4 options de calcul disponibles dans hydra,
- les étapes de paramétrage des modes de calcul affinés,
- une présentation
¶ Les modes de résolution des équations de Barré de Saint Venant par Hydra
Les équations de St Venant sont reproduites ci-dessous pour mémoire (cf. manuel d’analyse) en deux et une dimension respectivement :
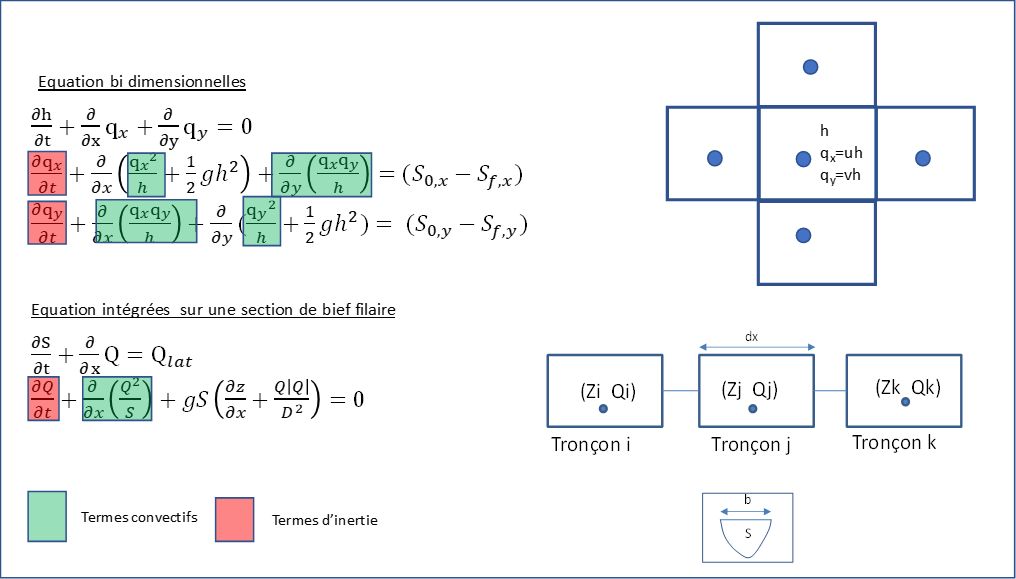
Les modes de calculs peuvent être classés en quatre grandes familles :
¶ 1. Formulation simplifiée (par défaut)
C’est la formulation par défaut dans Hydra : les termes convectifs et les termes d’inertie sont négligés. Cette simplification est licite pour les classes de problèmes dominés par les forces de pression, les forces de pesanteur et les termes de friction. Sur un plan numérique elle présente l’avantage de résoudre des systèmes matriciels limités à un degré de liberté : la cote d’eau à chaque nœud de calcul, ce qui implique des réductions importantes des temps de calcul. Par ailleurs l’algorithme de résolution mis en œuvre dans Hydra pour cette classe d’équations est très robuste.
¶ 2. Formulation complète (Affin)
Dans cette formulation, tous les termes des équations ci-dessus sont pris en compte : le système mathématique d’équations est de nature hyperbolique; cela signifie en pratique qu’il peut engendrer des solutions intégrant des discontinuités dans certaines configurations, se traduisant par des chocs hydrauliques (ressauts et intumescences). La prédiction de ces chocs et de leurs caractéristiques est de grande importance dans certains problèmes d’ingénierie : un choc s’accompagne de fortes turbulences et pose des problèmes de sécurité sur les personnes et les biens dans le cas de ruptures accidentelles d’ouvrages ou de défauts brusques de fonctionnement d’équipement (coupure d’alimentation d’une station de pompage par exemple).
Dans les applications courantologiques 2D, outre les chocs, la formulation complètes assure le couplage des termes convectifs croisés et permet ainsi de modéliser correctement les courants de recirculation en aval d’obstacles.
La résolution complète des équations ci-dessus met en œuvre un système d’équations avec trois inconnues interdépendantes par maille pour une schématisation bi-dimensionnelle, et deux inconnues par tronçon pour une schématisation filaire. Par ailleurs les chocs étant caractérisés par de forts gradients de hauteur d’eau et de vitesse, leur capture nécessite une discrétisation spatiale assez fine du domaine modélisé (la taille d’une maille doit typiquement être comprise entre un mètre et 10 mètres de côté ).
Les pas de temps sont généralement ajustés à la taille des mailles et sont donc assez faibles :
- avec la méthode de résolution explicite, la condition de Courant : doit être satisfaite pour assurer la convergence des calculs,
- avec la méthode de résolution implicite mise en œuvre dans Hydra cette condition n’est pas requise, mais le pas de temps doit néanmoins être contrôlé pour restituer les gradients de part et d’autre des chocs avec une précision adéquate. Ce contrôle est fait automatiquement via la procédure de pas de temps adaptatif implantée dans Hydra.
Ce mode de calculs ne doit être activé que si la physique du problème le nécessite. Les temps de calculs sont en effet plus longs et leur robustesse n’est pas aussi forte que dans le cas précédent.
¶ 3. Formulation complète avec gestion des bancs découvrants (Affin with dry land)
La méthode de calcul complète (méthode Affin) fonctionne bien dans le domaine 2D tant qu’il y a une hauteur minimum d’eau sur chacune des mailles du domaine.
Dans le cas d’un cours d’eau modélisé en 2D ou dans le cas d’un estuaire, les niveaux d’eau varient selon le débit amont ou le niveau de marée. Il en résulte des mises à découvert et des recouvrements périodiques de mailles au cours d’une même simulation, avec pour conséquence des réductions importantes des pas de temps de calcul.
Plusieurs formulations différentes ont été testées dans Hydra pour tenter de résoudre ce problème. La méthode trouvée la plus performante consiste à désactiver les termes convectifs dès que le niveau d’eau sur une maille devient inférieur à 10cm et de maintenir ces termes désactivés dans la suite de la simulation. Dans cette méthode les termes d’inertie restent actifs pour toutes les mailles. Les temps de calculs ne sont alors pratiquement pas affectés.
Cette formulation s’avère particulièrement satisfaisante pour modéliser les phénomènes de masses d’eau oscillantes que l’on rencontre dans les milieux estuariens. Elle doit par contre être proscrite dans les problèmes de rupture de barrages ou de protection de berges car le lit majeur qui reçoit l’onde de rupture est initialement sec. Dans ce cas le traitement des termes convectifs est réglé dans le code pour moduler l’action de ces termes pour les faibles hauteurs d’eau sans pour autant les désactiver : il se trouve que le code fonctionne bien si le lit majeur inondable se remplit ou se vide sans que la cote d’eau ne soit contrôlée par une condition de forçage externe, telle qu’une condition de marée.
¶ 4. Formulation allégée (Inertia terms only)
Cette formulation correspond à la formulation simplifiée avec en plus la prise en compte des termes d’accélération, ou, de façon équivalente, à la formation complète moins les termes convectifs.
Elle présente les mêmes avantages de rapidité et de robustesse des calculs que dans la formulation simplifiée. Sa mise en œuvre s’avère nécessaire dans les modélisations d’ondes longues en régime transitoire, telles que les ondes de marée, pour assurer une reproduction correcte des vitesses de propagation de ces ondes. Les mécanismes physiques sont en effet dominés par les termes de gravité et les termes d’inertie pour ce type de problèmes.
Elle doit en revanche être proscrite pour les modélisations courantes en réseau d’assainissement où l’on rencontre fréquemment des situations de régimes transitoire suite à des mouvements d’actionneurs : le terme d’inertie engendre alors des oscillations parasites non physiques, car en réalité les termes convectifs s’opposent à ces oscillations. Une formulation complète serait alors nécessaire pour modéliser très précisément ces phénomènes transitoires ponctuels dans le temps. En pratique leur modélisation a très peu d’incidence sur le comportement hydraulique global du réseau, c’est la raison pour laquelle on ignore le plus souvent ces phénomènes en appliquant la formulation simplifiée.
¶ Les classes de problèmes et les formulations associées
Les problèmes pratiques impliquant de la modélisation hydraulique à surface libre peuvent être regroupés en plusieurs grandes familles :
¶ 1. L’assainissement urbain
La modélisation des réseaux d’assainissement a pour objet de dimensionner des réseaux, d’établir des schémas directeurs et des diagnostics globaux de fonctionnement, de faire des bilans et de fournir des prévisions d’apports pour les systèmes d’aide à la gestion des flux.
Un réseau d’assainissement comprend généralement de très nombreux ouvrages qui interfèrent avec les écoulements dans les collecteurs.
Les équations simplifiées de Barré de St Venant suffisent dans la très grande majorité des cas pour traiter ces différentes questions avec une précision suffisante vis-à-vis des réponses cherchées.
¶ 2. Propagation et débordements dans les vallées alluviales
Les phénomènes fluviaux que l’on cherche à modéliser sont des phénomènes lents et sont dominés par les termes de frottement, de pression et de gravité. Les phénomènes d’inondation et de propagation d’écoulement dans les plaines inondables sont généralement modélisés avec une précision suffisante à l’aide des équations simplifiées de Barré de St Venant. Les échanges entre domaines (plaines inondables, biefs, casiers de surstockage), sont bien représentés par les lois de surverse paramétrables, sans qu’il soit nécessaire de calculer précisément les conditions d’écoulement à leur voisinage (lames d’eau torrentielles locales sur des ruptures de pentes, etc…).
¶ 3. Etudes courantologiques locales
Ces études reposent sur une modélisation bidimensionnelle d’un cours d’eau pour étudier les interférences des écoulements avec un ouvrage (pont, seuil déversant) et les conséquences sur la répartition des courants et les risques d’érosion. Ce type d’étude est souvent couplé avec l’analyse morphologique et la modélisation hydro-sédimentaire.
Pour ce type de problème, la résolution des équations complètes de St Venant est une nécessité, pour permettre de modéliser correctement les zones privilégiées d’écoulement, les chemins de recirculation et les forces tractrices génératrices de mouvements hydro-sédimentaires.
La carte ci-dessous montre un exemple des rouleaux de recirculation à l’aval du barrage de Couloisy (rivière Aisne), engendrés par l’effet de jet de la chute d’eau à l’aval immédiat du barrage :
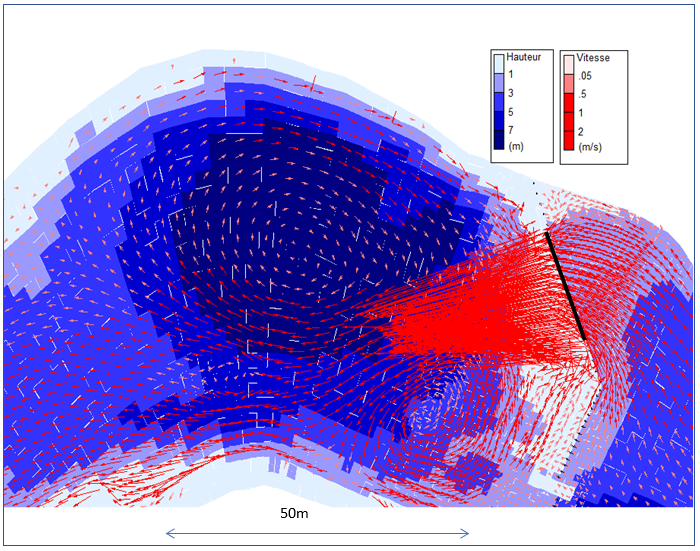
Les zones de recirculation sont générées par la prise en compte des termes convectifs croisés de l’équation de quantité de mouvement de Barré de St Venant. Une modélisation simplifiée n’aurait pas permis d’engendrer de telles zones de recirculation.
¶ 4. Etudes locales 1D – conceptions d’ouvrages
Les ouvrages de type vanne ou seuil génèrent fréquemment des changements de régime hydraulique : écoulements torrentiels en sortie de vanne ou en aval d’un seuil, au sein de biefs en condition fluviale, ou exhaussements en amont conduisant à des ressauts sur des tronçons torrentiels. Dans certains cas, la connaissance de ces changements de régime est fondamentale pour appréhender la loi de débitance de l’ouvrage, notamment lorsqu’un écoulement torrentiel local en aval dénoie un seuil, un orifice, une vanne.
Ces interactions sont illustrées par l’exemple suivant d’une vanne implantée en aval immédiat dans un canal de 5 m de large avec une forte pente en amont.
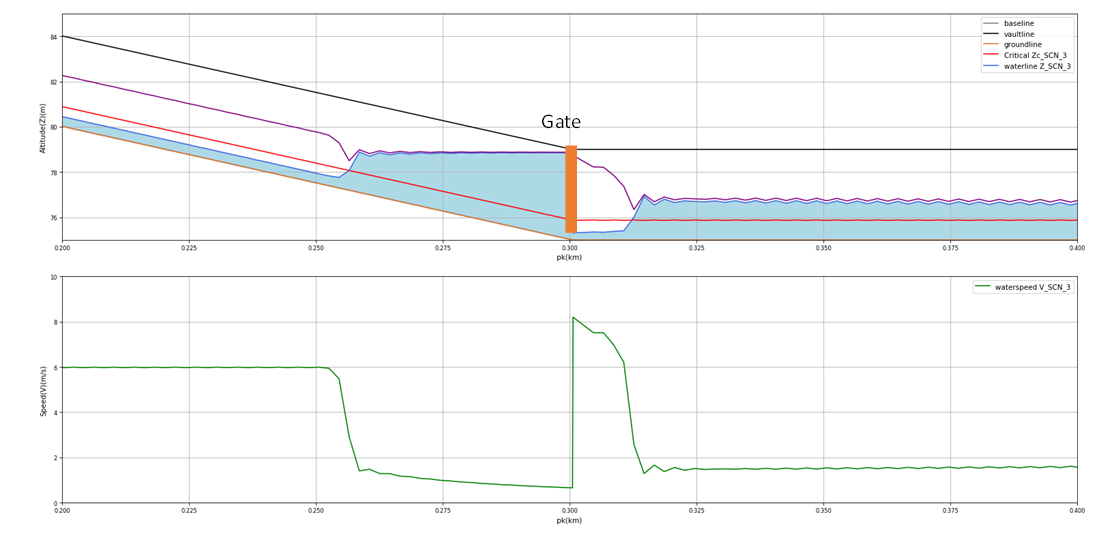
En amont de la vanne, le niveau est contrôlé par l’écoulement sous la vanne et crée un ressaut hydraulique sur le bief à forte pente.
En aval, l’écoulement sous la vanne provoque le décollement de la lame d’eau : la vanne ne voit pas le niveau loin en aval et reste dénoyée du fait de la ligne d’eau supercritique générée par la contraction.
Avec la formulation simplifiée le niveau d’eau aval reste « collé » contre la vanne, forçant une loi de débitance en régime noyé, et risque de fausser les résultats si le niveau aval est supérieur à la cote du seuil. Le calcul simplifié risque dans ce cas de générer une ligne d’eau amont beaucoup plus élevée.
Les analyses locales fines d’interaction d’ouvrages avec les lignes d’eau dans des collecteurs ou des canaux peut donc nécessiter des calculs précis, faisant appel à une exploitation complète des équations de St Venant.
¶ 5. Phénomènes hydrauliques transitoires rapides
Ces phénomènes sont générés par des ruptures d’ouvrages ou des pannes brutales d’organes électromécaniques. Ils se traduisent généralement par la formation d’une intumescence qui ne peut être décrite que par les équations complètes de St Venant. Les applications pratiques usuelles sont l’onde de rupture de barrage, l’intumescence provoqué par une éclusée ou l’arrêt brutal du pompage à l’aval d’un canal.
On peut également évoquer la création d’une onde de submersion en plaine inondable résultant d’une brèche dans une digue bordant un cours d’eau. Dans ce dernier cas, la formation ou non d’une intumescence va dépendre d’un certain nombre de facteurs, en particulier la largeur finale de la brèche, sa durée d’ouverture et le volume d’eau déversé pendant cette période.
¶ 6. Modélisation des phénomènes estuariens
Comme précisé plus haut, il est dans ce cas indispensable d’inclure le terme d’inertie dans la formulation simplifiée afin de restituer correctement les temps de propagation de l’onde de marée.
Note
De cette rapide analyse il ressort que la nécessité ou non de recourir à une formulation complète des équations de Barré de St Venant dépend de la classe de problème considéré. Pour une classe donnée il peut être nécessaire de traiter une partie du modèle avec la formulation complète, le reste pouvant être modélisé avec une formulation simplifiée. Dans tous les cas une analyse préliminaire du problème posé est nécessaire pour sélectionner la solution de modélisation la plus adaptée.
¶ Paramétrage des modes de calcul affinés
¶ Gestionnaire de scénario
Par défaut c’est la méthode simplifiée qui est appliquée dans Hydra. On précise ci-après comment paramétrer les méthodes Affinées.
Le paramétrage est activé via le gestionnaire de scénario, dans la fenêtre computation options/Upgrade computation.
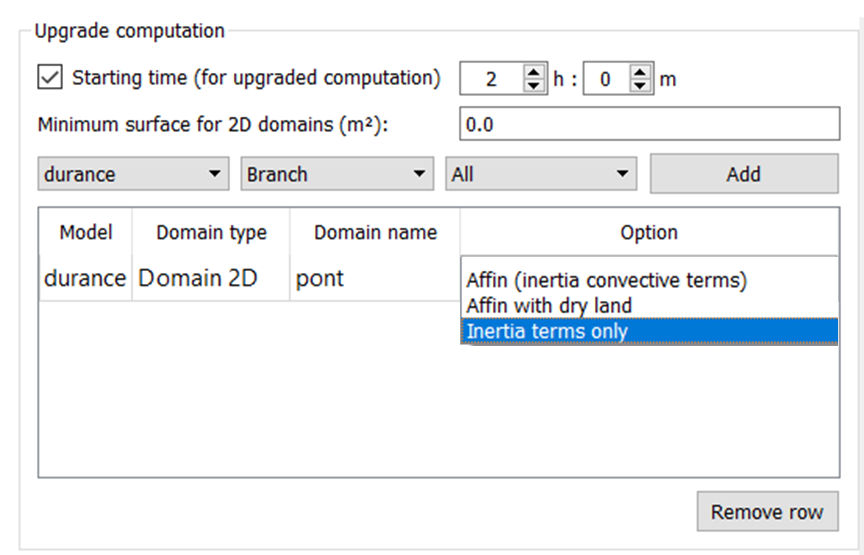
Il faut tout d’abord :
- Cocher la case « Upgrade computation »,
- Définir un temps relatif pour le démarrage des calculs en mode AFFIN. Les calculs démarrent en effet toujours en mode simplifié.
Il faut ensuite appeler les noms des sous-domaines que l’on souhaite traiter en mode Affiné. On retrouve dans le menu déroulant les trois catégories de domaine : domain 2D, reach, branch. L’utilisateur doit sélectionner le modèle, le type de domaine et le nom du sous-domaine dans cette catégorie. L’option All permet d’activer le calcul Affiné pour tous les sous-domaines de même type.
Il suffit ensuite de valider la sélection avec le bouton Add. Un bouton Remove permet de retirer un sous-domaine de cette liste.
Le bouton Options permet de sélectionner le mode de calcul à appliquer :
- Affin (inertia convective terms) : Calcul complet
- Affin with dry lands : Calcul complet mais désactivation des termes d’inertie pour toutes les mailles découvrantes au cours de la simulation
- Inertia terms only : Prise en compte des termes d’accélérations seul, les termes convectifs sont ignorés.
Lors de l’exécution des calculs le programme activera le mode Affiné sélectionné pour tous les sous-domaines listés dans cet écran de saisie, les autres domaines continuant d’être traités par le mode simplifié.
Note
le champ minimum surface for 2D domain peut être activé pour accélérer la vitesse de résolution des équations en régime établi impliquant des domaines 2D. Il convient en pratique de limiter la valeur de ce paramètre à 10 ou 20 m² au maximum.
¶ Attribution de noms à des sous-domaines
Les objets de modélisation pouvant être nommés sont les éléments constitutifs des domaines 2D (coverage), les biefs de rivière (reach) et les branches de collecteurs (branch). Ces éléments constitutifs sont appelés des sous-domaines.
Les sous-domaines 2D ne sont pas automatiquement nommés lors de leur création (le champ « Nom » est vide par défaut), ce qui n’a pas de conséquences sur le calcul. Un nom unique peut être attribué à plusieurs sous-domaines 2D, pour les besoins du calcul AFFIN ou d’autres utilisations.
En revanche, des noms sont automatiquement attribués aux sous-domaines filaires « reach » et « « branch lors de leur création. Ces noms peuvent être appelés lors du paramétrage du mode AFFIN. Ils sont également personnalisables par l’utilisateur à sa convenance, à condition que chaque sous-domaine ait un nom différent.
Les paragraphes pages suivantes détaillent la procédure d’attribution de nom pour chaque type de sous-domaine.
¶ Le sous-domaine 2D
Pour connecter un coverage à un nom de domaine on procède comme suit :
- Un nouveau nom de domaine est défini via le bouton « manage 2d Domain » dans la liste des objets d’Hydra.
- Le bouton « 2d domain » est sélectionné et posé à l’intérieur d’un « coverage ». L’utilisateur sélectionne le nom de sous-domaine qu’il souhaite attacher au coverage par l’intermédiaire du bouton « 2d domain ».
- Le coverage est ensuite maillé. Après cette opération, toutes les mailles du coverage portent le nom du domaine 2D défini dans l’objet « 2d domain »
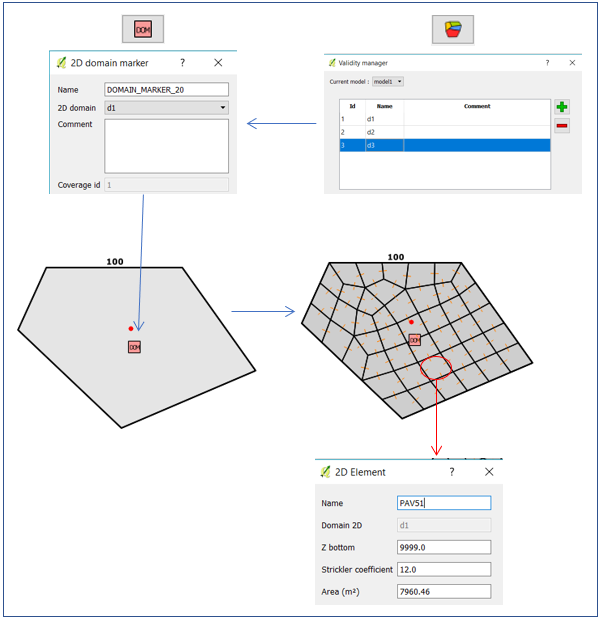
Il est possible, via cette procédure, d’attacher un nom de sous-domaine commun à plusieurs « coverage ». Une simple requête via l’éditeur de Qgis permet de visualiser tous les « coverage » partageant le même nom.Par ailleurs un « coverage » peut n’être attaché à aucun nom de domaine (c’est le cas par défaut).
¶ Le bief filaire
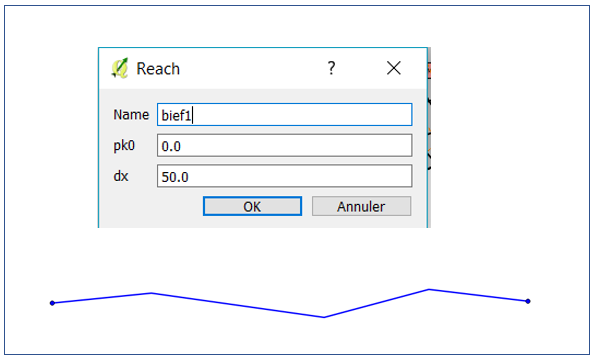
Le bief filaire (reach) est un objet Hydra représentant un bief de cours d’eau ou de vallée. Chaque bief porte un nom défini au moment de sa création.
Ce nom est personnalisable dans le menu de paramétrage de l’objet reach. Dans ce même menu, on peut également modifier le pas de discrétisation « dx » des nœuds de calculs en phase d’exécution (la valeur dx = 50 m est définie par défaut).
¶ La branche de collecteur
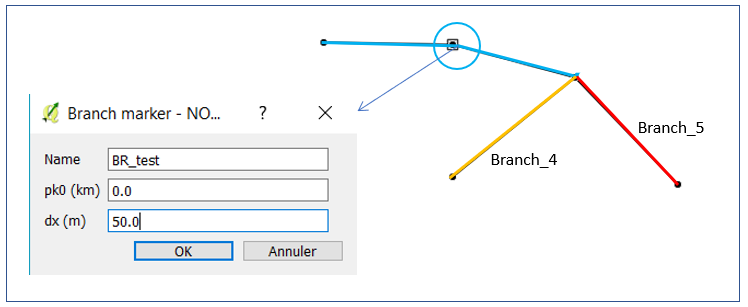
Les branches de collecteurs sont générées automatiquement par le plugin au fur et à mesure de la construction du modèle filaire. A chaque branche le programme affecte par défaut un nom et un pas de discrétisation dx (50 m) qui sont susceptibles d’être modifiés au cours de la construction. Ce pas d’espace doit être réduit si le mode Affin est activé.
Afin de modifier ce paramètre il suffit de poser l’objet « branch marker » sur n’importe quel nœud appartenant à la branche et de redéfinir la pas d’espace avec l’éditeur de l’objet.
¶ Précisions sur les calculs au droit des singularités et des liaisons entre domaines
¶ Rappel des conditions de calcul par défaut
Pour les équations de plein champ, utilisées au sein de chaque domaine homogène, la formulation simplifiée est utilisée par défaut (mise à zéro des termes convectifs).
Pour les singularités, la formulation simplifiée est également activée par défaut, mais la schématisation employée intègre un affinage compensant la perte d’information :
- La plupart des lois de singularités prennent en compte les charges hydrauliques et non les cotes
- Les lois prennent en compte les changements de régime au sein de la singularité, sauf lorsqu’ils interfèrent avec les termes convectifs des équations de plein champ.
L’utilisation de la formulation complète doit donc être « demandée » explicitement dans les secteurs qui le nécessitent. Ceci implique d’attribuer au préalable des noms à ces secteurs (étape décrite dans le paragraphe suivant), noms qui seront appelés dans le menu de paramétrage des options de calcul.
¶ Traitement des singularités
Les équations présentées ci-dessus sont des équations dites « de plein champ », elles sont utilisées au sein de chaque sous-domaine homogène (maillage 2D au sein d’un même coverage, bief 1D d’un tronçon de rivière, branche de collecteur).
Une complication dans la résolution des équations complètes vient de la présence des singularités, qui constituent les interfaces entre sous-domaines, et qui interfèrent avec les équations de plein champ ci-dessus. Chaque singularité est caractérisée par une équation de la forme Q=f (H1, H2), où H désigne la charge hydraulique. Il faut généralement pour chaque singularité considérer plusieurs configurations possibles selon la nature des régimes d’écoulement en amont et en aval de la singularité. La formulation appliquée dans Hydra est adaptée en conséquence (cf. manuel d’analyse hydraulique) et donne des résultats satisfaisants comme le démontrent les applications traitées dans le manuel de validation.
Da façon schématique la formulation des singularités dans Hydra s’adapte automatiquement à la formulation retenue pour chaque domaine.
¶ Traitement des flux de quantité de mouvement aux interfaces entre domaines
Les domaines sont connectés entre eux par des liaisons (links). Chaque liaison fait transiter un débit via la loi de la singularité Q (H1, H2) mais aussi un vecteur flux de quantité de mouvement dont l’expression diffère selon la nature des domaines connectés et le type de formulation sélectionné pour chaque domaine.
Malgré la grande diversité de configurations possibles, le nombre de cas à traiter peut être ramené à 9 en considérant une combinaison de trois indices. Chaque indice caractérise la nature et le mode de traitement retenu pour une maille ou un nœud connecté à la liaison. La liaison se voit donc attribuer deux indices (un pour l’amont, un pour l’aval). Ceci est effectué dans la phase de lecture des données.
Indice 1 : cet indice est appliqué dans les cas suivants :
- nœud courant de domaine filaire (par opposition aux nœuds d’extrémité),
- maille appartenant à un domaine traité en mode simplifié.
- casier,
- carrefour
- nœud de station de gestion.
Indice 2 : nœud extrémité d’une branche ou d’un bief traité en mode AFFIN.
Indice 3 : maille d’un domaine 2D traité en mode AFFIN.
Les cas de figure possibles sont récapitulés dans le tableau suivant :

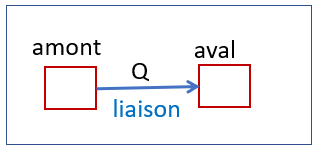
Dans ce tableau le premier champ désigne l’indice affecté au nœud amont, le second champ désigne l’indice affecté au nœud aval. Le principe de calcul du flux ne dépend pas de l’orientation du flux dans la liaison, les formulations étant symétriques. Le schéma conceptuel est donc le suivant.

¶ Précautions et recommandations pratiques
¶ Discrétisation spatiale
Pour les sous-domaines pour lesquels la méthode Affiné est appliquée il faut généralement limiter le pas de discrétisation spatial à 5 ou 10 m maximum pour les domines filaires de façon à reproduire correctement les chocs hydrauliques éventuels. Concernant le domaine 2D la taille d’une maille doit être comprise entre 5 et 20 m pour un calcul correct du champ de vitesse.
¶ Effets de bord
Dans le domaine 2D, la prise en compte des termes convectifs et le calcul des flux de quantité de mouvement se traduit par la modélisation de l’inertie des masses d’eau. Il convient donc, une fois le besoin identifié, d’étendre le champ de modélisation en mode Affiné suffisamment loin en amont et en aval du secteur d’étude de façon que ces phénomènes soient correctement modélisés là où les résultats vont être exploités.
En première approche, on peut retenir des linéaires amont et aval :
- De 2 à 3 fois la largeur au miroir de part et d’autre pour les études courantologiques impliquant tout le lit mineur,
- De 10 fois la dimension caractéristique des singularités ponctuelles (piles de pont), en l’absence d’autres perturbations.
¶ Robustesse des calculs
¶ Cas du régime établi
Le mode Affiné doit toujours être activé après stabilisation des calculs en mode simplifié. Le temps de démarrage du calcul Affiné doit être ajusté en conséquence.
¶ Cas du régime transitoire rapide
Il convient d’activer le mode Affiné avant le démarrage du régime transitoire rapide.
La modification brutale de l’état de fonctionnement d’un actionneur va générer des conditions initiales propices à la formation d’une intumescence. Ce paramétrage est réalisé par l’intermédiaire d’un fichier externe de contrôle : la commande d’actionneur doit être complétée par le mot clé ‘TREACS’ entre quotes, suivi de la durée en secondes que l’on souhaite imposer pour atteindre le nouvel état.
Dans l’exemple ci-dessous, le seuil du déversoir ‘DE’ est abaissé en 2 secondes de la position initiale à la nouvelle position zs=100. Cette manœuvre est commandée à partir de l’instant t=1h.

Si le mot clé est omis, la même manœuvre sera exécutée, mais avec un temps d’exécution très supérieur, imposé par le programme, compatible avec un fonctionnement graduellement varié, mais incompatible avec la formation d’une intumescence.
Dans la version actuelle d’Hydra, 4 types d’objets reconnaissent le mot clé TREACS :
- L’objet Weir,
- L’objet L-Weir,
- L’objet Pump,
- L’objet Pump_deriv.
Avec ces objets on peut simuler par exemple :
- La génération d’une onde de rupture de barrage,
- La génération d’une intumescence à la suite d’une coupure brutale d’alimentation électrique d’une station de pompage.
Il reste à compléter cette liste par l’imposition d’une manœuvre brutale d’une vanne (le développement est en cours).